Mathematics 216 Computer-oriented Approach to Statistics
Self-Tests
Self-Test 1
Overview
It is important that you work through all the exercises in the unit self tests. They are designed to, along with the unit assignments, help you master the content presented in each unit. No grades are assigned to the self tests.
Each unit self-test has two parts: one on theory (A) and one on computer work (B). Working through these will help you review key exercises in the unit, which will help you prepare for assignments and exams.
NOTE: Solutions are provided for all exercises in the self-tests; this allows you to check your work.
Self-Test 1A. Theory Component
The Theory Component questions are designed to help you prepare for the theory portion of Assignment 1, and do not receive a grade. This component consists of two chapter quizzes in your eText.
Before proceeding, briefly review the Learning Objectives for the topics (listed below) presented in Unit 1:
- Overview of Statistics
- Data Classification
- Data Collection and Experimental Design
- Frequency Distributions and Their Graphs
- More Graphs and Displays
- Measures of Central Tendency
- Measures of Variation
- Measures of Position
The Learning Objectives are displayed at the start of each eText chapter topic section in the Study Guide. We suggest that you print these Learning Objectives, as well as the quizzes for Chapter 1 and Chapter 2. To print the Learning Objectives, click on each chapter topic in Unit 1 of the Study Guide. With the Learning Objectives displayed, click “Ctrl+P” and print the appropriate pages.
Each Chapter Quiz is located near the end of the relevant eText chapter in the eText. To print the quizzes:
- Navigate to the quiz in the eText.
- Press Ctrl+P (the print command)[1] on your keyboard if you have downloaded the eText; or click on the print icon if you are online.
- In the window that comes up, type the page numbers you wish to print.
- Press Continue.
- Press OK in your printer window.
Textbook Chapter 1 Quiz
Work through the Chapter 1 Quiz in your eText.
Write out step-by-step solutions for each question. This will allow you to review your work when you are preparing for your assignments and exams. Check your answers against the solutions provided.
Textbook Chapter 2 Quiz
Work through the Chapter 2 Quiz in your eText.
Write out step-by-step solutions for each question. This will allow you to review your work when you are preparing for your assignments and exams. Check your answers against the solutions provided.
Textbook Quiz Solutions
To see the solution for each quiz question in the eText, navigate the table of contents to locate Odd Answers.
Detailed solutions for the chapter quizzes are found in the Student’s Solutions Manual through Pearson MyLab. On the left-side navigation bar, click Chapter Contents > Student’s Solutions Manual.
Self-Test 1B. Computer Component
The Self‑Test1B problems are designed to help you prepare for the computer component of Assignment 1 and the midterm exam. These self-tests do not count for marks.
Before working through this self-test, we recommend you review the chapter computer labs. You should then be ready to complete the following computer objectives:
Computer Objective 1. Given the responses to a survey, create a StatCrunch data file that contains qualitative and quantitative variables. Save the StatCrunch data file in a My Data folder on the StatCrunch website.
Reference: Computer Lab 1
Computer Objective 2. Given a StatCrunch data file, recode the values of any given qualitative variable. Copy and paste a few rows of the recoded variables from the StatCrunch data table to a word processing document. Resave as a PDF file.
Reference: Computer Lab 1
Computer Objective 3. Given a StatCrunch survey data file, use tools of descriptive statistics to analyze the qualitative variables in the survey. These tools include: bar charts, pie charts, and mode. Copy and paste the numeric and graph analysis into a word processing document that can be converted to a PDF file. Resave as a PDF file.
Reference: Computer Lab 1
Computer Objective 4. Given a StatCrunch survey data file, use tools of descriptive statistics to analyze the quantitative variables in the survey. These tools include: histograms, box-and-whisker plots, mean, median, mode, standard deviation, variance, first quartile, third quartile, and interquartile range.
Reference: Computer Lab 1
Computer Objective 5. Given a StatCrunch survey data file, use tools of descriptive statistics to analyze subsets of survey variables.
Reference: Computer Lab 1
Computer Objective 6. Generate a set of random numbers, given a minimum and maximum value.
Reference: Computer Lab 1
Instructions
Use StatCrunch and a single word processing document to generate and save all of your solutions.
- Create your word processing document and call it Self‑Test1B. Save all your solutions in this file. (Be sure to use a word processing software that will allow you to later convert your document to PDF.)
- Type the main heading Self‑Test1B.
- Type the problem subheadings (Problem 1a, Problem 4b, etc.) into the file.
- As you work through the self-test computer problems, use StatCrunch to generate all computer-related solutions. Do not round off the results you get from StatCrunch.
- For each computer problem, copy and paste the output generated by StatCrunch into the Word file Self‑Test1B under the appropriate subheading.
- Type your solutions to the interpretation questions into the Word file Self‑Test1B, under the appropriate subheading.
- Each time you make a change to a StatCrunch file or to your word processing file, remember to save using the same file name.
- Check your answers. For the final solution to each problem, as well as key guided solution steps, see Self‑Test1B Solutions. Simply close that document to return to the problems page.
- We suggest that you print the computer objectives and computer problems and insert them in your notes. This will help you prepare for your assignments and your exams.
Self-Test 1B Problems
At this point you may wish to print out the Computer Objectives and Instructions displayed above, as well as the Computer Problems for Self Test 1B below, as follows. Press “Ctrl+P” and then, based on the page preview that appears, print the appropriate pages.
Once you have worked through the problems in this self-test, see Self‑Test1B Solutions to check your work.
Problem 1. Create a data file and a solutions file.
The owners of TastyExpress distributed the survey (Figure 1) to regular customers. Twenty-five regular customers responded to this survey, and their responses are detailed in Figure 2. The owners have hired you to analyze the survey results using StatCrunch.
| Please circle the survey code or fill in the numeric amounts that apply to you below. |
Variable | Text Code |
| 1. Please indicate your gender. | Gender | |
| ☐ female | 1 | |
| ☐ male | 2 | |
| 2. Please indicate the level of satisfaction you experienced when you made your last visit to TastyExpress. |
Satisfy | Code |
| ☐ very satisfied | 1 | |
| ☐ satisfied | 2 | |
| ☐ less than satisfied | 3 | |
| 3. Do you frequently bring children to TastyExpress? | Child | Code |
| ☐ yes | 1 | |
| ☐ no | 2 | |
| 4. How often do you use TastyExpress Coupons? | Coupon | Code |
| ☐ frequently | 1 | |
| ☐ occasionally | 2 | |
| ☐ never | 3 | |
| Variable | Numeric Value | |
| 5. For a typical month, please estimate the amount you spend at TastyExpress. |
Spend | $ _______ |
| 6. How many times per month do you typically visit TastyExpress? | Visits | _______ |
| 7. Please indicate your monthly family income before taxes. | Income | $ _______ |
| 8. Please indicate your age. | Age | _______ |
Figure 1. TastyExpress survey.
| Cust. No. | Gender | Satisfy | Child | Coupon | Spend | Visits | Income | Age |
| 1 | 1 | 1 | 1 | 1 | 130 | 14 | 4000 | 29 |
| 2 | 1 | 1 | 1 | 1 | 195 | 15 | 4500 | 25 |
| 3 | 2 | 3 | 2 | 3 | 12 | 4 | 6250 | 44 |
| 4 | 1 | 2 | 1 | 1 | 260 | 14 | 3100 | 30 |
| 5 | 2 | 2 | 2 | 3 | 23 | 6 | 5250 | 37 |
| 6 | 1 | 1 | 1 | 1 | 175 | 12 | 4250 | 32 |
| 7 | 2 | 2 | 2 | 2 | 25 | 7 | 7000 | 41 |
| 8 | 1 | 1 | 1 | 2 | 180 | 13 | 4300 | 28 |
| 9 | 1 | 1 | 1 | 1 | 170 | 15 | 6100 | 26 |
| 10 | 2 | 3 | 1 | 3 | 15 | 7 | 7200 | 43 |
| 11 | 2 | 3 | 2 | 3 | 16 | 6 | 6900 | 46 |
| 12 | 1 | 1 | 1 | 1 | 185 | 15 | 5200 | 29 |
| 13 | 2 | 3 | 1 | 3 | 23 | 7 | 6800 | 44 |
| 14 | 1 | 1 | 1 | 2 | 215 | 13 | 5000 | 32 |
| 15 | 1 | 2 | 1 | 1 | 155 | 12 | 4400 | 30 |
| 16 | 2 | 3 | 2 | 3 | 12 | 5 | 6500 | 42 |
| 17 | 2 | 2 | 2 | 3 | 19 | 6 | 7700 | 41 |
| 18 | 1 | 1 | 1 | 1 | 225 | 16 | 5000 | 23 |
| 19 | 1 | 1 | 2 | 1 | 215 | 18 | 5400 | 26 |
| 20 | 1 | 2 | 1 | 1 | 149 | 12 | 5300 | 24 |
| 21 | 2 | 3 | 2 | 3 | 9 | 4 | 7350 | 42 |
| 22 | 1 | 2 | 1 | 1 | 255 | 13 | 4900 | 25 |
| 23 | 2 | 3 | 2 | 3 | 200 | 14 | 10500 | 40 |
| 24 | 2 | 3 | 2 | 3 | 15 | 5 | 7300 | 39 |
| 25 | 1 | 1 | 1 | 1 | 245 | 12 | 5300 | 23 |
Figure 2. Data file: TastyExpress
Create a StatCrunch data file called TastyExpress. Input the 25 customer responses to the TastyExpress survey (based on Figure 2).
In the file, create the variables: Gender, Satisfy, Child, Coupon, Spend, Visits, Income, and Age. (Do NOT include the first column, Cust. No. data, in the StatCrunch data table.)
Save the data file named TastyExpress to your My Data folder on the StatCrunch website. Then, sign out of StatCrunch.
Open a new word processing file and save it as Self‑Test1B. Type the main heading Self‑Test1B. Below the main heading, type Problem 1a. Keep this file open as you proceed to the next step.
Open the StatCrunch data file TastyExpress from your MyData Folder on the StatCrunch website.
Export all the variables and data from the StatCrunch file to a csv comma delimited (spreadsheet file).
Copy and paste all the variables and data in the csv comma delimited file (spreadsheet file) to your word processing file Self‑Test1B, under the subheading Problem 1a.
Save.
Open the StatCrunch data file TastyExpress from your MyData folder.
Export all the quantitative variables along with the first five data values for each quantitative variable from the StatCrunch file to a csv comma delimited file (spreadsheet file).
Copy and paste all the quantitative survey variables along with the first five data values (for each of the quantitative variables) from the csv comma delimited file (spreadsheet file) to your Word file Self‑Test1B, under the subheading Problem 1b.
Note: If you have problems exporting the variables and data to a spreadsheet file, you can copy and paste directly from the StatCrunch data table to your Word file Self‑Test1B.
Problem 2. Recode variables to text descriptions and export them to a spreadsheet file.
Before analyzing the qualitative variables in the TastyExpress survey, you will recode the responses to these variables to recognizable text descriptions. For example, instead of coding the Gender responses 1 for female and 2 for male, you will recode the 1 to Female and the 2 to Male in a new column called Recode(Gender).
Open the StatCrunch file you just created, TastyExpress, and recode each qualitative variable as shown in Figure 3 below.
| Variable | Original Code | New Code |
| Gender | 1 | Female |
| 2 | Male | |
| Satisfy | 1 | VSat |
| 2 | Sat | |
| 3 | LSat | |
| Child | 1 | Yes |
| 2 | No | |
| Coupon | 1 | Freq |
| 2 | Occas | |
| 3 | Never |
Figure 3. Recoding values for the qualitative variables in the TastyExpress file
Export all the recoded variables along with the first five data values for each recoded variable from the StatCrunch file to a csv comma delimited file (spreadsheet file).
Copy and paste all the recoded variables and the first five data values (for each of the recoded variables) from the csv comma delimited file (spreadsheet file) to your word processing file Self‑Test1B, under the subheading Problem 2.
Save the recoded StatCrunch data file under the File Name TastyExpress Recoded.
Note: If you have problems exporting the variables and data to a spreadsheet file, you can copy and paste directly from the StatCrunch data table to your word processing file Self‑Test1B, under the subheading Problem 2.
Problem 3. Create and interpret a pie chart.
Open the StatCrunch Recoded data file, TastyExpress Recoded. In the next few questions, you will use statistical options commonly used in analyzing responses to qualitative variables, such as pie charts, mode, bar plots.
- Use StatCrunch to create a pie chart for the variable Recode(Gender). Each slice of the pie should display the gender category’s relative frequency (percentage of total responses). Copy and paste the pie chart from the StatCrunch window to your word processing file Self‑Test1B, under the subheading Problem 3a.
- Based on the pie chart, which gender category was most frequently surveyed? Type your response under the heading Problem 3b.
Problem 4. Determine and interpret modes of qualitative variables.
Open the StatCrunch data file TastyExpress Recoded.
- Use StatCrunch to determine the modal response for each of the qualitative variables Satisfy, Child, and Coupon. Copy and paste the StatCrunch Summary Statistics Table (which displays the mode) to your word processing file Self‑Test1B, under the subheading Problem 4a.
- Under the subheading Problem 4b, type the mode for Satisfy, Child, and Coupon. Interpret the results in terms of the appropriate recoded values.
Problem 5. Create and interpret a Pareto chart.
Open the StatCrunch data file TastyExpress Recoded.
Use StatCrunch to create a Pareto chart summarizing the responses to the survey question about level of customer satisfaction.
Copy and paste the StatCrunch Pareto chart to your word processing file. Self‑Test1B, under the subheading Problem 5a.
- Does the Pareto chart indicate a relatively high or low level of customer satisfaction with TastyExpress? Explain. Type your explanation into your word processing file Self‑Test1B, under the subheading Problem 5b.
Problem 6. Create and interpret a frequency table.
Open the StatCrunch data file TastyExpress Recoded. In the next few questions, you will use statistical options commonly used to analyze the responses to quantitative variables: frequency and relative frequency tables with classes; histograms; measures of central tendency, variation, and position; and box-and-whisker plots.
- Use StatCrunch to create a frequency table summarizing the responses to the Age survey question. The frequency table should have 6 bins (classes) with a starting value of 20 and a fixed bin width of 5 where each bin includes the left endpoint. The frequency table should display: Frequencies, Relative Frequencies, and Cumulative Relative Frequencies. Copy and paste the frequency table to your word processing file Self‑Test1B, under the subheading Problem 6a.
- What customer age category (class) is the most frequent? Type your answer into the word processing file Self‑Test1B, under the subheading Problem 6b.
- Interpret the relative frequency of the second class. Type your answer into the word processing file Self‑Test1B, under the subheading Problem 6c.
- Interpret the cumulative relative frequency of the third class. Type your answer into the word processing file Self‑Test1B, under the subheading Problem 6d.
Problem 7. Create and interpret a histogram.
Open the StatCrunch data file TastyExpress Recoded.
Use StatCrunch to create a histogram summarizing the responses to the Visits survey question. The histogram should have 4 bins (classes) with a starting value of 0 and a fixed bin width of 5. The histogram should display the relative frequencies of each class.
Copy and paste the StatCrunch Histogram to your word processing file Self‑Test1B, under the subheading Problem 7a.
- What customer Visits category (class) is the most frequent? Type your answer in the word processing file Self‑Test1B, under the subheading Problem 7b.
- Interpret the relative frequency of the third class. Type your answer in the word processing file Self‑Test1B, under the subheading Problem 7c.
Problem 8. Analyze the variable Visits.
Open the StatCrunch data file TastyExpress Recoded.
- Use StatCrunch to determine the mean, median, standard deviation, first quartile, third quartile, and interquartile range for the variable Visits in the TastyExpress survey. Copy and paste the Summary Statistics Table displaying all these statistics to your word processing file Self‑Test1B, under the subheading Problem 8a.
- 75% of the customers visited TastyExpress more than ____ times per month. Type your answer in the word processing file Self‑Test1B, under the subheading Problem 8b.
Problem 9. Analyze the monthly visits.
Open the StatCrunch data file TastyExpress Recoded.
- Use StatCrunch to compute the mean and standard deviation monthly Visits for each of the gender subsets: male and female customers. In other words, compare the mean and standard deviation monthly visits made by the male customers with those made by the female customers. Copy and paste the Summary Statistics Table displaying these statistics to your word processing file Self‑Test1B, under the subheading Problem 9a.
- Which gender tends to visit TastyExpress more frequently? Type your answer into the word processing file Self‑Test1B, under the subheading Problem 9b.
Problem 10. Analyze the monthly amount spent.
Open the StatCrunch data file TastyExpress Recoded.
- Use StatCrunch to compute the mean and standard deviation monthly amount spent for each of the Gender subsets: male and female customers. In other words, compare the mean and standard deviation amount spent per month by females vs males at TastyExpress. Copy and paste the Summary Statistics table displaying these statistics to your word processing file Self‑Test1B, under the subheading Problem 10a.
- Which gender tends to spend more per month at TastyExpress? Type your answer into the word processing file Self‑Test1B, under the subheading Problem 10b.
Problem 11. Create and interpret box-and-whisker plots.
Open the StatCrunch data file TastyExpress Recoded.
Use StatCrunch to create two box-and-whisker plots that compare the monthly number of visits from customers who frequently bring children to TastyExpress with the monthly number of visits from customers who do NOT frequently bring children to TastyExpress.
Copy and paste the box-and-whisker plots to your word processing file Self‑Test1B, under the subheading Problem 11a.
Which subset tends to make more monthly visits to TastyExpress: customers who frequently bring children, or customers who do NOT frequently bring children?
Hint: Move your mouse pointer over each box plot to display a pop‑up window that shows the median monthly visits.
Type your answer into the word processing file Self‑Test1B, under the subheading Problem 11b.
Problem 12. Create and interpret a contingency table.
Open the StatCrunch data file: TastyExpress Recoded.
- Use StatCrunch to create a contingency table that examines the relationship between the two variables Recode(Gender) and Recode(Satisfy). Select Recode(Gender) as the row variable and Recode(Satisfy) as the column variable. Display the Row percents in the table. Copy and paste the contingency table from StatCrunch to the word processing file Self‑Test1B, under the subheading Problem 12a.
- Under the subheading 12b, type the relation that appears to exist between the variables Recode(Gender) and Recode(Satisfy), by focusing on the appropriate row percentages.
Problem 13. Simulate coin tossing.
Open a new StatCrunch blank data table.
Generate random integers to simulate tossing a coin 200 times. Let 1 represent heads and 2 represent tails. Allow repeats.
Copy and paste all the numbers generated in the StatCrunch Random Number Window to the first Variable Column in the blank data table, with the first pasted value in Row 1.
Type Coin as the name of this first variable.
Recode the 1 to show as Heads and the 2 to show as Tails and store the results in the second column, with the variable name displayed as Recode(Coin).
Create a frequency table for the variable Recode(Coin), which displays the frequency and relative frequency.
Copy and paste the frequency table from StatCrunch to the word processing file Self‑Test1B, under the subheading Problem 13a.
- Theoretically, you should expect to see the relative frequency of the Heads category to be close to ____%. Type your answer under the subheading Problem 13b. Because random integers are used in the solution, solutions will vary.
Footnote
[1] Keyboard shortcuts given in this course are for PC computers. If you are using a Mac computer, you will likely use the Command key rather than the Control key.
Self-Test 2
Overview
It is important that you work through all the exercises in the unit self-tests. No grades are assigned to the self-tests. They are designed to, along with the unit assignments, help you master the content presented in each unit.
Each unit self-test has two parts: one on theory (A) and one on computer work (B). Working through these will help you review key exercises in the unit, which will help you prepare for assignments and exams.
NOTE: Solutions are provided for all exercises in the self-tests; this allows you to check your work.
Self-Test 2A. Theory Component
The Theory Component questions are designed to help you prepare for the theory portion of Assignment 2, and do not receive a grade. This component consists of the chapter 3 quiz in your eText.
Before proceeding, briefly review the Learning Objectives for topics (listed below) presented in Unit 2:
- Basic Concepts of Probability and Counting
- Conditional Probability and the Multiplication Rule
- The Addition Rule
- Additional Topics in Probability and Counting
The Learning Objectives are displayed at the start of each eText chapter topic section in Unit 2 of the Study Guide. We suggest that you print these Learning Objectives, as well as the quiz for Chapter 3.
To print the Learning Objectives, click on each chapter topic located in Unit 2 of the Study Guide. With the Learning Objectives displayed, click “Ctrl+P” and then print the appropriate pages.
For help printing the chapter quiz, see Navigating Your eText on the course home page.
Textbook Chapter 3 Quiz
Work through the Chapter 3 Quiz in your eText.
Write out step-by-step solutions for each question. This will allow you to review your work when you are preparing for your assignments and exams. Check your answers against the solutions provided.
Textbook Quiz Solutions
To see the solution for each quiz question in the eText, navigate the table of contents to locate Odd Answers.
Detailed solutions for the chapter quizzes are found in the Student’s Solutions Manual through Pearson MyLab. On the left-side navigation bar, click Chapter Contents > Student’s Solutions Manual.
Self-Test 2B. Computer Component
The Unit 2 Self-Test Computer Component problems are designed to help you prepare for the computer component of Assignment 2 and the midterm exam. These self-tests do not count for marks.
Before working through this self-test, we recommend you review the chapter computer labs. You should then be ready to complete the following computer objectives:
Computer Objective 1. Derive probabilities involving one variable: Use StatCrunch to compute the relative frequency of an event after the related probability experiment has occurred numerous times. Use the rules of probability to compute other events based on the same experiment.
Reference: Computer Lab 2
Computer Objective 2. Derive probabilities involving multiple variables: Use StatCrunch to compute the appropriate contingency table. Use the rules of probability to compute other events based on the results displayed in the contingency table.
Reference: Computer Lab 2
Computer Objective 3. Use StatCrunch to simulate probability experiments and games of chance. Use StatCrunch to apply the concept of empirical probability to compute the probability of specific outcomes of a probability experiment. Use the rules of probability to compute other events based on the same experiment.
Reference: Computer Lab 2
Instructions
Use StatCrunch and a single Word file to generate and save all of your solutions.
- Create your word processing document and call it Self‑Test2B. Save all your solutions in this file. (Be sure to use a word processing software that will allow you to later convert your document to PDF.)
- Type the main heading Self‑Test2B.
- Type the problem subheadings (Problem 1a, Problem 4b, etc.) into the file.
- As you work through the self-test computer problems, use StatCrunch to generate all computer-related solutions. Do not round off the results you get from StatCrunch.
- For each computer problem, copy and paste the output generated by StatCrunch into the Word file Self‑Test2B.
- Type your solutions to the interpretation questions into the Word file Self‑Test2B.
- Each time you make a change to a StatCrunch file or to your Word file, remember to save.
- Check your solutions. For the final solution to each problem, as well as key guided solution steps, see Self‑Test2B Solutions.
- We suggest that you print the computer objectives and the computer problems and insert them in your notes. This will help you prepare for your assignments and your exams.
Self-Test 2B Problems
At this point you may wish to print out the Computer Objectives and Instructions displayed above, as well as the Computer Problems for Self Test 2B below, as follows. Press “Ctrl+P” and then, based on the page preview that appears, print the appropriate pages.
Problem 1. Work with random numbers and probability.
Consider the probability experiment of tossing one die and observing the number that comes up.
Use StatCrunch to generate random numbers between 1 and 6, to simulate the tossing of one die 500 times.
Open a new StatCrunch data table.
Copy and paste all the numbers generated in the Random numbers window into the first variable column in the blank data table, with the first pasted value in Row 1.
Type Die as the name of this first variable. Save the data table to the MyData folder under the file name OneDie.
Open a new word processing file and save it as Self‑Test2B. Type the main heading Self‑Test2B. Below the main heading, type Problem 1a. Keep this file open as you proceed to the next step.
Copy and paste the first five rows of data for the variable Die (along with the variable name at the top of the column) from the StatCrunch data file OneDie to the Word file Self‑Test2B, under the subheading Problem 1a.
Referring to Problem 1a above, consider this event: The die number that comes up will be at least 3. This number could be 3, 4, 5, or 6.
The complementary event is: The die number that comes up will be less than 3. This number could be 1 or 2.
Using the data file OneDie, approximate the probability of the event that the die number will be at least 3, based on the empirical concept of probability. That is, use StatCrunch to approximate the relative frequency related to the event “the die number will be at least 3,” based on repeating the probability experiment 500 times as you did in Problem 1a.
Hint: With the data file OneDie open, create the recoded variable Recode(Die) with two values: “at least 3” and “less than 3”. That is, recode the die numbers 3, 4, 5, and 6 as “at least 3”, and the numbers 1 and 2 as “less than 3”.
Create a relative frequency table for the variable Recode(Die) that displays the relative frequency for the two values “at least 3” and “less than 3”.
Copy and paste the two variable names, Die and Recode(Die), and the first five values for each of these variables from StatCrunch to the Word file Self‑Test2B, under the subheading Problem 1b.
Copy and paste the frequency table that you created to the Word file Self‑Test2B, under the subheading Problem 1b. Based on your frequency table created, Probability (at least 3) =_____?
Save the StatCrunch data file as OneDie and the Word file Self‑Test2B.
Theoretically (based on the classical view of probability), you should expect to see the relative frequency of the “At Least 3” category to be close to ____?
Type your answer under the subheading Problem 1c. Because random integers are used in the solution, solutions will differ depending on the student.
Problem 2. Probability and random numbers
Consider the following probability experiment. A pair of dice is tossed and you are interested in observing the total of the two numbers that come up on the dice.
For example, if a pair of ones (1,1) appears, the total is 2. If the two dice show a 5 on the first die and 3 on the second die (5,3) the total is 8.
Open a new StatCrunch blank data table. Use StatCrunch to simulate this probability experiment of tossing a pair of dice simultaneously 1000 times by doing the following:
Use StatCrunch to generate random numbers, between 1 and 6, so as to simulate tossing one die 1,000 times. Copy and paste all the numbers generated in the StatCrunch Random Number Window to the first Variable Column in the blank data table, with the first pasted value in Row 1. Type Die1 as the name of this first variable.
Repeat the above process for the second Variable column in the data table. That is, use StatCrunch to generate random numbers, between 1 and 6, so as to simulate tossing a second die 1,000 times. Copy and paste all the numbers generated in the StatCrunch Random Number Window to the second Variable Column in the blank data table, with the first pasted value in Row 1. Type Die2 as the name of this second variable.
For each row in the data table, you want StatCrunch to total the numbers in variable columns 1 and 2 and store the result in a third new variable column entitled Die1+Die2.
Hint: To start the process of creating this new variable column, click on the menu options: Data → Compute → Expression (see the Guided Solution for more details).
After generating the variable column Die1+Die2, copy and paste the variable names and the first five rows of columns Die1, Die2, and Die1+Die2 from StatCrunch to the Word file Self‑Test2B, under the subheading Problem 2a.
Save the StatCrunch data file as TwoDice and the Word file Self‑Test2B.
Refer to the probability experiment in Problem 2a, in which a pair of dice is tossed and the total of the two numbers that appear is observed. Consider the event “the dice total will be at least 10.” This means that the dice total could be 10, 11, or 12.
Theoretically, the probability of “the dice total will be at least 10” is calculated as follows:
Overall, the sample space related to tossing 2 dice consists of 36 possibilities: ((1,1)...(1,6), (2,1)...(2,6), (3,1)...(3,6), (4,1)...(4,6), (5,1)...(5,6), (6,1)...(6,6)).
The number of outcomes associated with “the dice total will be at least 10” are: ((4,6), (5,5), (6,4),(5,6), (6,5), (6,6))
Using the StatCrunch data that you created in Problem 2a above, use StatCrunch to approximate the probability of the event “the dice total will be at least 10” based on the empirical concept of probability. That is, you want StatCrunch to compute the relative frequency related to the event “the dice total will be at least 10” based on repeating the probability experiment 1,000 times as you did in problem 2a.
Hint: With the StatCrunch file TwoDice open and the variable Die1+Die2 displayed in the third column, create the Recoded Variable Recode(Die1+Die2) with two values: “At Least 10” and “Less Than 10”. That is, recode the totals 10, 11, and 12 as “At Least 10”; and the eight totals 2 through 9 as “Less Than 10”.
Use StatCrunch to create a frequency table for the variable Recode(Die1+Die2) that displays the relative frequency for the two values “At Least 10” and “Less Than 10”.
Copy and paste the four variable names, Die1, Die2, Die1+Die2, and Recode(Die1+Die2), with the first five values for each of these variables to the Word file Self‑Test2B, under the subheading Problem 2b.
Copy and paste the frequency table that you created to, the Word file Self‑Test2B, under the subheading Problem 2b. Based on your frequency table created, the Probability (At Least 10) = _____?
Save the StatCrunch data file as TwoDice and the Word file Self‑Test2B.
Theoretically (based on the classical view of probability), you should expect to see the relative frequency of the “At Least 10” category to be close to ____?
Type your answer in the Word file Self‑Test2B, under the subheading Problem 2c. Because random integers are used in the solution, solutions will differ.
Problem 3. Relative frequency of an event
Open the TwoDice worksheet data that you created in problem 2 above.
Use StatCrunch to approximate the probability of the event “the dice total will be at most 5” based on the empirical concept of probability. That is, you want StatCrunch to compute the relative frequency related to the event “the dice total will be at most 5” based on repeating the probability experiment 1,000 times as you did in Problem 2 above.
Hint: First note that the event “the dice total will be at most 5” includes the mutually exclusive totals: 2, 3, 4, or 5.
With the StatCrunch file TwoDice open and the variable Die1+Die2 displayed in the third column, create a second recoded variable Recode(Die1+Die2) with two values : “At Most 5” and “More Than 5”. That is, recode the totals 2, 3, 4, and 5 as “At Most 5”. Similarly, recode the seven totals 6 through 12 as “More Than 5”.
Use StatCrunch to create a frequency table for the second recoded variable Recode(Die1+Die2) that displays the relative frequency for the two values “At Most 5” and “More Than 5”.
Copy and paste the frequency table that you created from StatCrunch to the Word file Self‑Test2B, under the subheading Problem 3a. Based on your frequency table created, the Probability (At Most 5) =_____?
Save the StatCrunch data file TwoDice and the Word file Self‑Test2B.
Theoretically (based on the classical view of probability) you should expect to see the relative frequency of the “At Most 5” category to be close to ____?
Type your answer under the subheading Problem 3b. Because random integers are used in the solution, solutions will differ depending on the student.
Problem 4. Sun Exposure survey
In this and subsequent problems, you will use the actual responses made by 4022 Canadians in Canada's first and only national Sun Exposure Survey, to determine and compute probabilities of interest.
Figure 1 presents two questions from the Sun Exposure Survey. Figure 2 provides an overview of the actual responses received from the 4022 Canadians. These responses are stored in the StatCrunch file called SunEx1, which is located in the Groups folder AU Math216 2020.
| Please circle the coded responses that apply to you. | Variable | Code |
| 1. Was the diagnosed pre-cancerous condition malignant melanoma (skin cancer?) |
Melanoma | |
| ☐ Yes | 1 | |
| ☐ No | 2 | |
| ☐ Was never diagnosed with pre-cancer | 3 | |
| ☐ Do not know | 4 | |
| ☐ Not stated | 5 | |
| 2. Would you say your natural skin colour is (on your inner arm) | SkinColour | |
| ☐ Light (white, or fair, or ruddy) | 1 | |
| ☐ Medium (olive, light/medium brown) | 2 | |
| ☐ Dark (dark brown, black) | 3 | |
| ☐ Do not know (or refused to say) | 4 |
Figure 1: Adapted from Selected Survey Questions: Canadian Sun Exposure Survey. Source: Section 12.0, Questionnaire. 1996 Sun Exposure Survey. The National Study on Sun Exposure and Protective Behaviours. Funded by: National Cancer Institute of Canada, The Canadian Dermatology Association, The Canadian Association of Optometrists, Environment Canada, Health Canada, BC Tel. (Special Surveys Division Division des enquêtes spéciales, Statistics Canada, Ottawa, Ontario, Canada, 1996).
| Respondent Number | Melanoma | SkinColour |
| 1 | 3 | 2 |
| 2 | 3 | 1 |
| 3 | 3 | 1 |
| 4 | 3 | 2 |
| 5 | 3 | 2 |
| . | . | . |
| . | . | . |
| . | . | . |
| 4019 | 3 | 2 |
| 4020 | 3 | 2 |
| 4021 | 3 | 2 |
| 4022 | 3 | 2 |
Figure 2. Data File: SunEx1. To check your understanding of the data table above, the first Canadian responding to the survey (Respondent Number 1) has not been diagnosed with melanoma and has medium skin colour.
Recode the responses.
Open the StatCrunch dataset file SunEx1, which is in the StatCrunch Groups folder AU Math216 2020. Recode each of the coded responses to the variables Melanoma and SkinColour to more recognizable values, as shown in Figure 3. The recoded values will be displayed as new column variables Recode(Melanoma) and Recode(SkinColour).
After recoding the variables, copy and paste the first 5 rows (along with the variable names) of the two recoded variable columns Recode(Melanoma) and Recode(SkinColour)-C2 from the StatCrunch data table to the Word file Self‑Test2B, under the subheading Problem 4a.
Save the StatCrunch data file as TwoDice and the Word file as Self‑Test2B.
Variable Original Code: New Code: Melanoma 1
2
3
4
51-Yes
2-No
3-NeverDiag
4-DoNotKnow
5-NotStatedSkinColour 1
2
3
41-Light
2-Medium
3-Dark
4-DoNotKnowFigure 3: Recode Data Values in SunEx1 data table.
Use StatCrunch to construct a contingency table consisting of the two recoded variables Recode(Melanoma) and Recode(SkinColour).
Select Recode(Melanoma) as the row variable and Recode(SkinColour) as the column variable. Display both the Counts and Row Percents.
Copy and paste the contingency table that you created from StatCrunch to the Word file Self‑Test2B, under the subheading Problem 4b.
- Based on the contingency table you created, use your calculator (not StatCrunch) to compute the probability that a randomly selected adult Canadian responding to the survey will have the following attributes:
- have light skin colour
- have been diagnosed with malignant melanoma
- have medium skin colour or will be diagnosed with malignant melanoma
- have dark skin colour and will be diagnosed with malignant melanoma
- have light skin colour, given that they have been diagnosed with malignant melanoma
- determine, by making the appropriate math calculations, if the events “light skin colour” and “have been diagnosed with malignant melanoma” are independent events.
Type your answers under Problem 4c in your Word file.
Save the StatCrunch data file TwoDice and the Word file Self‑Test2B.
Self-Test 3
Overview
It is important that you work through all the exercises in the unit self-tests and the eText chapter quizzes. No grades are assigned to the self-tests. They are designed to, along with the unit assignments, help you master the content presented in each unit.
Each Unit Self-Test is divided into two portions, one on theory (A) and one on computer work (B). This will help you review key exercises for the theory and computer components of the unit, and will help you prepare for assignments and exams.
NOTE: Solutions are provided for all exercises in the self-tests; this allows you to check your work.
Self-Test 3A. Theory Component
The Theory Component questions are designed to help you prepare for the theory portion of Assignment 3. This component consists of two chapter quizzes in your e‑textbook.
Before proceeding, briefly review the Learning Objectives for the topics (listed below) presented in Unit 3:
- Probability Distributions
- Binomial Distribution
- Introduction to Normal Distributions
- Normal Distributions: Finding Probabilities
- Normal Distributions: Finding Values
The Learning Objectives are displayed at the start of each eText chapter topic section in Unit 3 of the Study Guide. We suggest that you print these Learning Objectives, as well as the quizzes for Chapters 4 and 5.
To print the Learning Objectives, click on each chapter topic located in Unit 3 of the Study Guide. With the Learning Objectives displayed, click “Ctrl+P” and then print the appropriate pages.
If you need help printing the chapter quiz, see “Printing Chapter Quizzes” in Navigating Your eText on the course home page.
Textbook Chapters 4 and 5 Quizzes
Work through the quizzes for Chapters 4 and 5 of your eText. In the Chapter 4 quiz, omit questions 5, 6, 7. In the Chapter 5 quiz, omit questions 9, 10, 11, 12.
Write out step-by-step solutions for each question. This will allow you to review your work when you are preparing for your assignments and exams. Check your answers against the solutions provided.
Textbook Quiz Solutions
To see the solution for each quiz question in the eText, navigate the table of contents to locate Odd Answers.
Detailed solutions for the chapter quizzes are found in the Student’s Solutions Manual through Pearson MyLab. On the left-side navigation bar, click Chapter Contents > Student’s Solutions Manual.
Self-Test 3B. Computer Component
The Unit 3 Self-Test Computer Component problems are designed to help you prepare for the computer component of Assignment 3 and the midterm exam. These self-tests do not count for marks.
Before working through this self-test, we recommend you review the unit computer labs. You should then be ready to complete the following computer objectives:
Computer Objective 1. With the probability distribution of a discrete random variable displayed in a StatCrunch data table, find the mean and standard deviation of a discrete random variable.
Computer Objective 2. Use StatCrunch to compute binomial probabilities, given n, p, and x.
Computer Objective 3. Use StatCrunch to simulate the playing of roulette and to compute the average long run payoff.
Computer Objective 4. Use StatCrunch to compute normal probabilities, given the mean and standard deviation.
Computer Objective 5. Use StatCrunch to compute X values, given the related normal probability.
Instructions
Use StatCrunch and a single word processing document to generate and save all of your solutions.
- Create your word processing document and call it Self‑Test3B. Save all your solutions in this file. (Be sure to use a word processing software that will allow you to later convert your document to PDF.)
- Type the main heading Self‑Test3B.
- Type the problem subheadings (Problem 1a, Problem 4b, etc.) into the file.
- As you work through the self-test computer problems, use StatCrunch to generate all computer-related solutions. Do not round off the results you get from StatCrunch.
- For each computer problem, copy and paste the output generated by StatCrunch into the Word file Self‑Test3B.
- Type your solutions to the interpretation questions into the Word file Self‑Test3B.
- Each time you make a change to a StatCrunch file or to your Word file, remember to save.
- Check your solutions. For the final solution to each problem, as well as key guided solution steps, see Self‑Test3B Solutions.
- We suggest that you print the computer objectives and computer problems and insert them in your notes. This will help you prepare for your assignments and your exams.
Self-Test 3B Problems
Note: Where relevant, do NOT round off the results you get from StatCrunch.
Once you have worked through the problems in this self-test, see Self‑Test3B Solutions to check your work.
Problem 1. Dozens Bet in roulette
You may recall that, in the game of roulette, the roulette wheel contains 38 equally sized spaces. The wheel is spun and a ball randomly lands in one of these spaces. Two spaces are green and have numbers 0 and 00 on them. The other spaces are numbered from 1 to 36.
In this problem you will focus on the probability distribution related to placing a one-dollar Dozens Bet in roulette. With this bet, you will bet on the roulette ball falling either on a number from 1 to 12, 13 to 24, or 25 to 36. In this bet, you will receive 2:1 odds, which means that if you win, you will receive a net payoff of 2 × $1 = $2, and you will get your $1 back in addition to this net payoff. If the ball does not fall on one of these three number sets, you will lose $1 or receive a net payoff of $−1.
Assuming that each time you play the Dozens Bet, you will bet that the roulette ball will stop at a number between 1 and 12; and that the probability of winning will be (12/38) or 0.3158 and the probability of losing will be (26/38) or 0.6842. Figure 1 below describes the probability distribution related to this type of roulette bet.
| Net Payoff, X | $2 | $−1 |
| P(X) | 0.3158 | 0.6842 |
Figure 1. Probability distribution of Dozens Bet in roulette
Create the data table DozensBet, and the Word file SeftTest3B.
Open a new StatCrunch data table.
Create two variables: NetPayoff and P(X).
Enter the values for these two variables, as shown in Figure 1.
Save this probability distribution table in StatCrunch with the title DozensBet.
Open a new word processing file and save it as Self‑Test3B. Type the main heading Self‑Test3B. Below the main heading, type Problem 1a. Keep this file open as you proceed to the next step.
Copy and paste the Dozens Bet probability distribution table that you created in StatCrunch into the Word file Self‑Test3B, under the subheading Problem 1a.
Use StatCrunch to compute the mean and standard deviation of the probability distribution related to the Dozens Bet.
Copy and paste the Graph, Mean and Standard Deviation of the Dozens Bet probability distribution created in StatCrunch into the Word file Self‑Test3B, under the subheading Problem 1b.
Save your files.
- From a practical viewpoint, interpret the meaning of the mean that StatCrunch computed in question 1b. Type your answer under the subheading Problem 1c.
Problem 2. Multiple-choice test
You are about to complete a 100-question multiple-choice test. Each question offers 4 answer options (a, b, c, and d), but only one option is the correct answer. Because you know nothing about the subject matter being tested. you will randomly select what you hope is the correct answer option for each question.
Before you start the test, you are going to use StatCrunch to compute the following probabilities. You can assume the binomial distribution, as for each question there are two outcomes, correct answer chosen or incorrect answer chosen, with the probability of choosing the correct answer for each question being (1/4) = 0.25.
Answer the following problems based on your completion of the 100-question test:
- Find the probability of getting exactly 50 correct answers. Copy and paste the graph and the probability into your Word file Self‑Test3B, under the subheading Problem 2a.
- Find the probability of getting at most 40 correct answers. Copy and paste the graph and the probability into your Word file, Self‑Test3B under the subheading Problem 2b.
- Find the probability of getting less than 30 correct answers. Copy and paste the graph and the probability into your Word file, Self‑Test3B, under the subheading Problem 2c.
- Find the probability of getting more than 80 correct answers. Copy and paste the graph and the probability into your Word file, Self‑Test3B, under the subheading Problem 2d.
- Find the probability of getting between 20 and 30 correct answers. Copy and paste the graph and the probability into your Word file, Self‑Test3B, under the subheading Problem 2e.
- Find the probability of passing the exam (50 or more correct answers). Copy and paste the graph and the probability into your Word file, Self‑Test3B, under the subheading Problem 2f.
Problem 3. Knee transplant
Suppose, in a large hospital, that the number of days spent waiting for a knee transplant (called the “waiting time”) is approximated by a normal distribution with a mean of 122 days with a standard deviation of 34 days. Consider the next patient, who has just been informed that she needs a hip transplant.
- Find the probability that the waiting time will be at least 120 days. Copy and paste the graph and the probability into your Word file, Self-Test3B, under the subheading Problem 3a.
- Find the probability that the waiting time will be at most 90 days. Copy and paste the graph and the probability into your Word file, Self‑Test3B, under the subheading Problem 3b.
- Find the probability that the waiting time will be less than 60 days. Copy and paste the graph and the probability into your Word file, Self‑Test3B, under the subheading Problem 3c.
- There is a 90% probability that the waiting time will be at least how many days? Copy and paste the graph and the probability into your Word file, Self‑Test3B, under the subheading Problem 3d.
- There is an 85% probability that the waiting time will be at most how many days? Copy and paste the graph and the probability into your Word file, Self‑Test3B, under the subheading Problem 3e.
Self-Test 4
Overview
It is important that you work through all the exercises in the unit self-tests and the eText chapter quizzes. Note that neither the self-tests nor the chapter quizzes are assigned marks. They are designed to, along with the unit assignments, help you master the content presented in each unit.
Each Unit Self-Test is divided into two portions, one on theory (A) and one on computer work (B). This will help you review key exercises for the theory and computer components of the unit, and will help you prepare for assignments and exams.
NOTE: Solutions are provided for all exercises in the self-tests; this allows you to check your work.
Self-Test 4A. Theory Component
The Theory Component questions are designed to help you prepare for the theory portion of Assignment 4. This component consists of two chapter quizzes in your e‑textbook.
Before proceeding, briefly review the Learning Objectives for the topics (listed below) presented in Unit 4:
- Sampling Distributions and the Central Limit Theorem
- Confidence Intervals for the Mean (σ known)
- Confidence Intervals for the Mean (σ unknown)
- Confidence Intervals for Population Proportions
- Introduction to Hypothesis Testing with One Sample
- Hypothesis Testing for the Mean (σ known)
- Hypothesis Testing for the Mean (σ unknown )
- Hypothesis Testing for Proportions
We suggest that you print these Learning Objectives, as well as the quizzes for Chapter 6 and Chapter 7. Check your solutions. (For help printing the chapter quizzes, see Navigating Your eText on the course home page.)
Textbook Chapter 6 Quiz
Work through the Chapter 6 Quiz in your eText. Omit question 7.
Write out step-by-step solutions for each question. This will allow you to review your work when you are preparing for your assignments and exams. Check your answers against the solutions provided.
Textbook Chapter 7 Quiz
Work through the Chapter 7 Quiz in your eText. Omit question 6.
Write out step-by-step solutions for each question. This will allow you to review your work when you are preparing for your assignments and exams. Check your answers against the solutions provided.
When you are doing Chapter 7, for each of the hypotheses tests below:
- Display HO and HA in mathematical terms.
- Determine whether the hypothesis test is one-tailed or two-tailed and whether to use a z‑test or t‑test.
- Sketch the sampling distribution, showing the critical value(s) and the rejection region.
- Compute the appropriate standardized test statistic.
- Determine whether you should reject or fail to reject the null hypothesis.
- Interpret your decision in the context of the original claim.
(List adapted from Larson, 01/2014, p. 410)
Textbook Quiz Solutions
To see the solution for each quiz question in the eText, navigate the table of contents to locate Odd Answers.
Detailed solutions for the chapter quizzes are found in the Student’s Solutions Manual through Pearson MyLab. On the left-side navigation bar, click Chapter Contents > Student’s Solutions Manual.
Self-Test 4B. Computer Component
The Self‑Test4B problems are designed to help you prepare for the computer component of Assignment 4 and the final exam. These self-tests do not count for marks.
Before working through this self-test, we recommend you review the chapter computer labs. You should then be ready to complete the following computer objectives:
Computer Objective 1. With the population probability distribution of a discrete random variable displayed in a StatCrunch data file, use StatCrunch to find the mean and standard deviation of the population distribution and display its graph.
Computer Objective 2. Use StatCrunch to approximate the graph, mean, and standard deviation of a sampling distribution of sample means through simulation.
Computer Objective 3. Use StatCrunch to compute confidence intervals for the population mean when the population standard deviation is known.
Computer Objective 4. Use StatCrunch to compute confidence intervals for the population mean when the population standard deviation is unknown.
Computer Objective 5. Use StatCrunch to find the minimum required sample size to estimate a population mean.
Computer Objective 6. Use StatCrunch to compute a confidence interval for the population proportion.
Computer Objective 7. Use StatCrunch to find the minimum required sample size to estimate a population proportion.
Computer Objective 8. Use the four-step P‑value approach to conduct a hypothesis test for the population mean with the population standard deviation unknown. Use StatCrunch to compute the test statistic and related P‑value.
Computer Objective 9. Use the four-step P‑value approach to conduct a hypothesis test to check if the parent population is normally distributed. Use StatCrunch to compute the Shapiro-Wilk test statistic and related P‑value.
Computer Objective 10. Use the four-step P‑value approach to conduct a hypothesis test involving a single population proportion. Use StatCrunch to compute the test statistic and related P‑value.
Instructions
Use StatCrunch and a single Word file to generate and save all of your solutions.
- Create your word processing document and call it Self‑Test4B. Save all your solutions in this file. (Be sure to use a word processing software that will allow you to later convert your document to PDF.)
- Type the main heading Self‑Test4B.
- Type the problem subheadings (Problem 1a, Problem 4b, etc.) into the file.
- As you work through the self-test computer problems, use StatCrunch to generate all computer-related solutions. Do not round off the results you get from StatCrunch.
- For each computer problem, copy and paste the output generated by StatCrunch into the Word file Self‑Test4B.
- Type your solutions to the interpretation questions into the Word file Self‑Test4B.
- Each time you make a change to a StatCrunch file or to your Word file, remember to save.
- Check your solutions. For the final solution to each problem, as well as key guided solution steps, see Self‑Test4B Solutions.
- We suggest that you print the problems and insert them in your notes. This will help you prepare for your assignments and your exams.
Self-Test 4B Problems
Note: Where relevant, do NOT round off the results you get from StatCrunch.
Once you have worked through the problems in this self-test, see Self‑Test4B Solutions to check your work.
Problem 1. Population experiment
Consider the following population experiment. You write the population values 1,3,5,7, and 9 on separate slips of paper and place these in a hat. You then select one slip of paper in a random manner. Let the population random variable, X, be the number that you observe on the slip of paper selected. The probability distribution of X is described in Figure 1 below.
| X | 1 | 3 | 5 | 7 | 9 |
| P(X) | .20 | .20 | .20 | .20 | .20 |
Figure 1. Population distribution.
Create a probability distribution table, and the Word file Self‑Test4B. Open a new data file in StatCrunch. Create the two variables X and P(X) and enter the values for these two variables, as shown in Figure 1. Save this probability distribution table as U4_ST_Q1_PopnDist.
Create a new Word file named Self‑Test4B. Copy and paste the probability distribution table into the Word file Self‑Test4B under the subheading Problem 1a.
- Use StatCrunch to display the graph and compute the mean and standard deviation for the population distribution in problem 1a. Copy and paste the graph and mean and standard deviation from StatCrunch to the Word file Self‑Test4B under the subheading Problem 1b.
With the StatCrunch data file U4_ST_Q1_PopnDist open, use StatCrunch to generate 10,000 repetitions of the following sampling experiment.
Drawing on the population values 1,3,5,7, and 9, randomly select a sample of 3 values, with replacement, and observe the sample mean. StatCrunch will simulate this experiment 10,000 times, so that 10,000 sample means will be created in one column of the data file. Copy and paste the first 5 sample means (along with the variable name) to the Word file Self‑Test4B under the subheading Problem 1c.
- Use StatCrunch to compute the mean and standard deviation of the 10,000 sample means that you generated in 1c and re-save the StatCrunch file as U4_ST_Q1_PopnDist. Copy and paste the Summary Statistics window that displays the mean and standard deviation of the sampling distribution to the Word file Self‑Test4B under the subheading Problem 1d.
- Based on the Central Limit Theorem, the mean and standard deviation of the sampling distribution in problem 1d should approximate what values? Type your answer into the Word file Self‑Test4B under the subheading Problem 1e.
- Use StatCrunch to create a relative frequency histogram for the 10,000 sample means you generated in 1c. Copy and paste the relative frequency histogram to the Word file Self‑Test4B under the subheading Problem 1f.
- How does the shape of the relative frequency histogram created in Problem 1f compare to what one would expect to see based on the Central Limit Theorem? Type your answer into the Word file Self‑Test4B under the subheading Problem 1g.
Problem 2. Exercise 45 from Elementary Statistics, 6th edition
Exercise 45. Watching TV Using DVRs

From past studies the research council assumes that the population standard deviation is 4.3 minutes and the population of times is normally distributed.
The data is in the data file EX6_1-45.txt, which is available in the AU Math216 2020 group folder on the StatCrunch website. Based on this sample data:
- Open the StatCrunch data file EX6_1-45.txt. Use StatCrunch to construct a 90% confidence interval for the mean number of minutes that adults spend watching TV using a DVR, each day. Copy and paste the StatCrunch Confidence Interval Table created to the Word file Self‑Test4B under the subheading Problem 2a.
- Use StatCrunch to construct a 99% confidence interval for the mean number of minutes that adults spend watching TV using a DVR, each day. Copy and paste the StatCrunch Confidence Interval Table created to the Word file Self‑Test4B under the subheading Problem 2b.
- What can you conclude regarding the relationship between the confidence level and the width of the confidence interval? Type your answer in the Word file Self‑Test4B under the subheading Problem 2c.
Problem 3. Exercise 30 from Elementary Statistics, 6th edition
Exercise 30. Annual Earnings
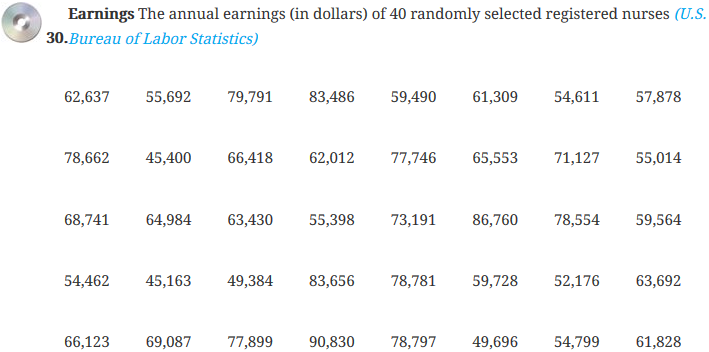
The annual earnings of 40 randomly selected registered nurses is in the data file EX6_2-30.txt, available in the StatCrunch group folder AU Math216 2020 at the StatCrunch website. Based on this sample data:
- Open the StatCrunch data file EX6_2-30.txt. Use StatCrunch to construct a 98% confidence interval for the mean annual earnings of the population of registered nurses. Copy and paste the StatCrunch Confidence Interval table created to the Word file Self‑Test4B under the subheading Problem 3a.
- Suppose the nurses’ union’s president recently complained that the average annual salary for registered nurses is below $60,000 per year (below levels earned in other jurisdictions). Test this claim with the confidence interval that you constructed in 3a. Type your answer in the Word file Self‑Test4B under the subheading Problem 3b.
- In constructing the confidence interval based on the sample of earnings for 40 randomly selected registered nurses, should you have first tested to see if the sample of earnings comes from a normally distributed population? Type your answer in the Word file Self‑Test4B under the subheading Problem 3c.
Problem 4. Exercise 50 from Elementary Statistics, 6th edition
Exercise 50. Ages of College Students
Assume that the population of ages is normally distributed and that the population standard deviation is 1.2 years.
- Use StatCrunch to determine the minimum sample size required to construct a 90% confidence interval with a maximum tolerable error of 1 year (E). Copy and paste the Confidence Interval Width window to the Word file Self‑Test4B under the subheading Problem 4a.
- Use StatCrunch to determine the minimum sample size required to construct a 99% confidence interval with a maximum tolerable error of 1 year (E). Type your answer in the Word file Self‑Test4B under the subheading Problem 4b.
- Which level of confidence requires a larger sample size (for the same tolerable error)? Type your answer in the Word file Self‑Test4B under the subheading Problem 4c.
Problem 5. Exercise 16 from Elementary Statistics, 6th edition
Exercise 16.

Use StatCrunch to construct a 90% confidence interval for the population proportion of adults who believe in UFOs. Copy and paste the StatCrunch Confidence Interval table created to the Word file Self‑Test4B under the subheading Problem 5.
Problem 6. Exercise 20 from Elementary Statistics, 6th edition
Exercise 20. Ice Cream

- Find the minimum sample size required, when no preliminary estimate is available. Copy and paste the StatCrunch Confidence Interval Width window to the Word file Self‑Test4B under the subheading Problem 6a.
- Find the minimum sample size required, when a preliminary study found that 28% of adults prefer chocolate ice cream over all other flavours. Copy and paste the StatCrunch Confidence Interval Width window to the Word file Self‑Test4B under the subheading Problem 6b.
Problem 7. Zoeys: Hypothesis Test
The manager of Zoeys, a fast food outlet, distributed the survey questionnaire (Figure 2) to its regular customers. Twenty-five regular customers responded, and their responses are stored in the StatCrunch file Zoeys available in the StatCrunch Math 216 group folder.
Zoeys Questionnaire:
| Please circle the survey code or fill in the numeric amounts that apply to you below. |
Variable | Text Code |
| 1. Please indicate your gender. | Gender | |
| ☐ female | 1 | |
| ☐ male | 2 | |
| 2. Please indicate the level of satisfaction you experienced when you made your last visit to Zoeys. |
Satisfy | Code |
| ☐ very satisfied | 1 | |
| ☐ satisfied | 2 | |
| ☐ less than satisfied | 3 | |
| 3. Do you frequently bring children to Zoeys? | Child | Code |
| ☐ yes | 1 | |
| ☐ no | 2 | |
| 4. How often do you use Zoeys Coupons? | Coupon | Code |
| ☐ frequently | 1 | |
| ☐ occasionally | 2 | |
| ☐ never | 3 | |
| Variable | Numeric Value | |
| 5. In a typical month, please estimate the amount that you spent at Zoeys. |
Spend | $ _______ |
| 6. How many times per month do you typically visit Zoeys? | Visits | _______ |
| 7. Please indicate your monthly family income before taxes. | Income | $ _______ |
| 8. Please indicate your age. | Age | _______ |
- Open the StatCrunch data file Zoeys. Test the hypothesis that the population mean family income for Zoey’s customers exceeds $5000 a month at a 5% level of significance. Use the four-step P‑value approach. Copy and paste the Hypothesis Test Results window from StatCrunch to the Word file Self‑Test4B under the subheading Problem 7a under Step 2 of the test.
- What assumption did you make in conducting the hypothesis test in 7a? Type your answer in the Word file Self‑Test4B under the subheading Problem 7b.
- Conduct the appropriate hypothesis test to determine if the sample of family incomes comes from a normal population. Use the four-step P‑value approach. Copy and paste the Hypothesis Test Results window from StatCrunch to the Word file Self‑Test4B under the subheading Problem 7c under Step 2 of the test.
Problem 8. Zoeys: Level of Significance
Refer to the Zoeys questionnaire. With the StatCrunch data file Zoeys open, use the four-step P‑value approach to test whether the population proportion of Zoeys customers who frequently use Zoeys coupons is at least 50% with a level of significance of 5%.
Hint: select the Column Variable Recode(Coupon) with “Success” being “Freq”. Copy and paste the Hypothesis Test Results window from StatCrunch to the Word file Self‑Test4B under the subheading Problem 8 under Step 2 of the test.
Self-Test 5
Overview
It is important that you work through all the exercises in the unit self-tests and the eText chapter quizzes. Note that neither the self-tests nor the chapter quizzes are assigned marks. They are designed to, along with the unit assignments, help you master the content presented in each unit.
Each Unit Self-Test is divided into two portions, one on theory (A) and one on computer work (B). This will help you review key exercises for the theory and computer components of the unit, and will help you prepare for assignments and exams.
NOTE: Solutions are provided for all exercises in the self-tests; this allows you to check your work.
Self-Test 5A. Theory Component
The Theory Component questions are designed to help you prepare for the theory portion of Assignment 1. This component consists of one chapter quiz in your e‑textbook.
Before proceeding, briefly review the Learning Objectives for each topic presented in Unit 5:
- Testing the Difference Between Means ( Independent Samples σ1 σ2 Known)
- Testing the Difference Between Means (Independent Samples σ1 σ2 not Known)
- Testing the Difference Between Means (Dependent Samples)
- Testing the Difference Between Proportions
We suggest that you print these Learning Objectives, as well as the quiz for Chapter 8. (For help printing the chapter quizzes, see Navigating Your eText on the course home page.)
Textbook Chapter 8 Quiz
For each of the hypotheses tests below:
- Display HO and HA in mathematical terms.
- Determine whether the hypothesis test is one-tailed or two-tailed and whether to use a z‑test or t‑test.
- Sketch the sampling distribution showing the critical value(s) and the rejection region.
- Compute the appropriate standardized test statistic.
- Determine if you should reject or fail to reject the null hypothesis.
- Interpret your decision in the context of the original claim.
Work through the Chapter 8 Quiz in your eText.
Write out step-by-step solutions for each question. This will allow you to review your work when you are preparing for your assignments and exams. Check your answers against the solutions provided.
Textbook Quiz Solutions
To see the solution for each quiz question in the eText, navigate the table of contents to locate Odd Answers.
Detailed solutions for the chapter quizzes are found in the Student’s Solutions Manual through Pearson MyLab. On the left-side navigation bar, click Chapter Contents > Student’s Solutions Manual.
The Self‑Test5B problems are designed to help you prepare for the computer component of Assignment 5 and the final exam. These self-tests do not count for marks.
Before working through this self-test, we recommend you review the chapter computer labs. You should then be ready to complete the following computer objectives:
Computer Objective 1. Test the hypothesis that two samples come from populations that have equal variances, four-step P‑value approach.
Computer Objective 2. Test the hypotheses involving two population means-two independent samples, population standard deviations unknown.
Computer Objective 3. Test the hypotheses involving two population means, two dependent samples, population standard deviation unknown.
Computer Objective 4. Test the hypotheses involving two population proportions, with the appropriate column variable (sample data) displayed in the data table.
Self-Test 5B
Instructions
Use StatCrunch and a single Word file to generate and save all of your solutions.
- Create your word processing document and call it Self‑Test5B. Save all your solutions in this file. (Be sure to use a word processing software that will allow you to later convert your document to PDF.)
- Type the main heading Self‑Test5B.
- Type the problem subheadings (Problem 1a, Problem 4b, etc.) into the file.
- As you work through the self-test computer problems, use StatCrunch to generate all computer-related solutions. Do not round off the results you get from StatCrunch.
- For each computer problem, copy and paste the output generated by StatCrunch into the Word file Self‑Test5B.
- Type your solutions to the interpretation questions into the Word file Self‑Test5B.
- Each time you make a change to a StatCrunch file or to your Word file, remember to save.
- Check your solutions. For the final solution to each problem, as well as key guided solution steps, see Self‑Test5B Solutions.
- We suggest that you print the problems and insert them in your notes. This will help you prepare for your assignments and your exams.
Self-Test 5B Problems
Note: Where relevant, do NOT round off the results you get from StatCrunch.
Once you have worked through the problems in this self-test, see Self‑Test5B Solutions to check your work.
Problem 1. Exercise 21 from Elementary Statistics, 6th edition
Exercise 21. Teaching Methods

The reading test scores of each group are saved in the StatCrunch data file Ex8_2-21.txt, available in the StatCrunch Math 216 group folder. At a 10% level of significance, conduct a hypothesis test to see if the mean reading scores under the new curriculum exceed the mean reading scores under the old curriculum. Assume that the two samples come from populations with equal variances.
- Open the StatCrunch file Ex8_2-21.txt. Use the four-step P‑value approach to test whether the mean reading scores under the new curriculum exceed the mean reading scores under the old curriculum at a 10% level of significance. Assume equal population variances when conducting the test (i.e. select the pooled variance option). Copy and paste the Hypothesis Test Results window to the Word file Self‑Test5B under the subheading Problem 1a under Step 2 of the test.
- What assumption did you make in conducting the hypothesis test in 1a? Type your answer in the Word file Self‑Test5B under the subheading Problem 1b.
- Conduct the appropriate hypothesis test, at alpha = 0.05, to determine whether each of the two samples of reading scores comes from a normal population. Use the four-step P‑value approach. Copy and paste the Hypothesis Test Results window to the Word file Self‑Test5B under the subheading Problem 1c under Step 2 of the test.
- Conduct the appropriate hypothesis test, at alpha = 0.05, to determine if the two samples of reading scores comes from populations with equal variances. Use the four-step P‑value approach. Copy and paste the Hypothesis Test Results window from StatCrunch to the Word file Self‑Test5B under the subheading Problem 1d under Step 2 of the test.
- Referring to Problem 1a, use StatCrunch to construct two separate 90% confidence intervals: one interval based on the sample of reading scores from the old curriculum, and the second interval based on the sample of reading scores from the new curriculum. Copy and paste both confidence intervals to the Word file Self‑Test5B under the subheading Problem 1e.
- Do the two confidence intervals created support your hypothesis test conclusion in Problem 1a? Type your explanation in the Word file Self‑Test5B under the subheading Problem 1f.
Problem 2. Exercise 19 from Elementary Statistics, 6th edition
Exercise 19. Blood Cholesterol Levels
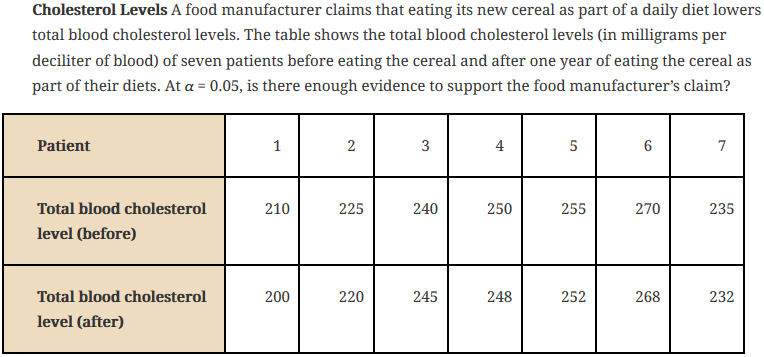
The data file Cereal, available in the StatCrunch Math 216 group folder, displays the blood cholesterol levels (in milligrams per deciliter of blood) for seven patients before they started eating the new cereal, and the blood cholesterol levels one year after they started eating the new cereal on a daily basis. At the 5% level of significance, is there enough evidence to support the manufacturer’s claim? Conduct the appropriate hypothesis test; make sure that you save the sample differences in order to test your assumptions in a subsequent problem.
- Open the StatCrunch data file Cereal. Use the four-step P‑value approach to test whether eating the new cereal daily lowers the mean blood cholesterol levels at a 5% level of significance. Copy and paste the Hypothesis Test Results window to the Word file Self‑Test5B under the subheading Problem 2a under Step 2 of the test.
- What key assumption was made when you tested the manufacturer’s claim in Problem 1a? Type your answer in the Word file Self‑Test5B under the subheading Problem 2b.
- At the 5% level of significance, test the hypothesis that the sample of differences comes from a population of differences that is normally distributed. Copy and paste the Hypothesis Test Results window from StatCrunch to the Word file Self‑Test5B under the subheading Problem 2b under Step 2 of the test.
Problem 3. Exercise 7 from Elementary Statistics, 6th edition
Exercise 7. Plantar Heel Pain

Of the 54 subjects who wore magnetic insoles, 17 felt mostly better. Of the 41 subjects who wore non-magnetic insoles, 18 felt mostly better. At a 1% level of significance, can you support the claim that there is a difference in the proportion of subjects who feel mostly better between the two groups? Use the four-step P‑value approach. Copy and paste the Hypothesis Test Results window from StatCrunch to the Word file Self‑Test5B under the subheading Problem 3 under Step 2 of the test.
Problem 4. Zoeys: Another Hypothesis Test
The manager of Zoeys, a fast food outlet, distributed the survey questionnaire to its regular customers. Twenty-five regular customers responded, and their responses are stored in the StatCrunch file Zoeys available in the StatCrunch Math 216 group folder.
Zoeys Questionnaire:
| Please circle the survey code or fill in the numeric amounts that apply to you below. |
Variable | Text Code |
| 1. Please indicate your gender. | Gender | |
| ☐ female | 1 | |
| ☐ male | 2 | |
| 2. Please indicate the level of satisfaction you experienced when you made your last visit to Zoeys. |
Satisfy | Code |
| ☐ very satisfied | 1 | |
| ☐ satisfied | 2 | |
| ☐ less than satisfied | 3 | |
| 3. Do you frequently bring children to Zoeys? | Child | Code |
| ☐ yes | 1 | |
| ☐ no | 2 | |
| 4. How often do you use Zoeys Coupons? | Coupon | Code |
| ☐ frequently | 1 | |
| ☐ occasionally | 2 | |
| ☐ never | 3 | |
| Variable | Numeric Value | |
| 5. In a typical month, please estimate the amount that you spent at Zoeys. |
Spend | $ _______ |
| 6. How many times per month do you typically visit Zoeys? | Visits | _______ |
| 7. Please indicate your monthly family income before taxes. | Income | $ _______ |
| 8. Please indicate your age. | Age | _______ |
Open the StatCrunch data file Zoeys. At a 5% level of significance, test the hypothesis that the population mean amount spent per month by the female customers at Zoeys exceeds the population mean amount spent per month by the male customers at Zoeys. Use the four-step P‑value approach. Copy and paste the Hypothesis Test Results window to the Word file Self‑Test5B under the subheading Problem 4a under Step 2 of the test. Use the pooled variance option when conducting this test.
Hint: Here, you are taking the one sample of 25 spending values and breaking it into two subset spending amounts: amounts spent by the female customers, and amounts spent by the male customers.
- What assumptions did you make in conducting the hypothesis test in 4a? Type your answer in the Word file Self‑Test5B under the subheading Problem 4b.
- Conduct the appropriate hypothesis test, at alpha = 0.05, to determine if the two subset samples, amounts spent by the female customers and amounts spent by the male customers, come from populations with equal variances. Use the four-step P‑value approach. Copy and paste the Hypothesis Test Results window from StatCrunch to the Word file Self‑Test5B under the subheading Problem 4c under Step 2 of the test.
- Conduct the appropriate hypothesis test to determine if both the subset samples, amounts spent by the female customers and amounts spent by the male customers, come from normal populations. Use the four-step P‑value approach. Copy and paste the Hypothesis Test Results window from StatCrunch to the Word file Self‑Test5B under the subheading Problem 4d under Step 2 of the test.
Problem 5. Zoeys: Population Proportion
Refer to the Zoeys questionnaire. With the StatCrunch data file Zoeys open, use the four-step P‑value approach to test whether the population proportion of Zoeys female customers who frequently use Zoeys coupons exceeds the population proportion of Zoeys male customers who frequently use Zoeys coupons, with a level of significance of 5%.
Hint: select the Column Variable Recode(Coupon) with “Success” being “Freq”. Copy and paste the Hypothesis Test Results window to the Word file Self‑Test5B under the subheading Problem 5 under Step 2 of the test.
Self-Test 6
Overview
It is important that you work through all the exercises in the unit self-tests and the eText chapter quizzes. Note that neither the self-tests nor the chapter quizzes are assigned marks. They are designed to, along with the unit assignments, help you master the content presented in each unit.
Each Unit Self-Test is divided into two portions, one on theory (A) and one on computer work (B). This will help you review key exercises for the theory and computer components of the unit, and will help you prepare for assignments and exams.
NOTE: Solutions are provided for all exercises in the self-tests; this allows you to check your work.
Self-Test 6A. Theory Component
The Theory Component questions are designed to help you prepare for the theory portion of Assignment 6. This component consists of two chapter quizzes in your e‑textbook.
Before proceeding, briefly review the Learning Objectives for the topics (listed below) presented in Unit 6:
- Correlation
- Linear Regression
- Measures of Regression and Prediction Intervals
- Test of Independence
- Analysis of Variance
We suggest that you print these Learning Objectives, as well as the quizzes for Chapters 9 and 10. Check your solutions. (For help printing the chapter quizzes, see Navigating Your eText on the course home page.)
Textbook Chapter 9 Quiz
Work through the Chapter 9 Quiz in your eText. Omit question 9.
Write out step-by-step solutions for each question. This will allow you to review your work when you are preparing for your assignments and exams. Check your answers against the solutions provided.
Textbook Chapter 10 Quiz
Only questions 2, 3, and 4 are assigned for the Chapter 10 quiz.
For question 2, use the age/education achievement table (page 576), which is a contingency table describing the educational attainment and age categories for the nation’s population. In conducting the hypothesis test for question 2, follow the following steps:
- Display HO and HA in mathematical terms.
- Sketch the sampling distribution showing the critical value(s) and the rejection region.
- Compute the appropriate standardized test statistic.
- Determine if you should reject or fail to reject the null hypothesis.
- Interpret your decision in the context of the original claim.
For questions 3 and 4, enter the data in StatCrunch and use the four-step P‑value approach to test the appropriate hypotheses.
Textbook Quiz Solutions
To see the solution for each quiz question in the eText, navigate the table of contents to locate Odd Answers.
Detailed solutions for the chapter quizzes are found in the Student’s Solutions Manual through Pearson MyLab. On the left-side navigation bar, click Chapter Contents > Student’s Solutions Manual.
Self-Test 6B
The Self‑Test6B problems are designed to help you prepare for the computer component of Assignment 6 and the final exam. These self-tests do not count for marks.
Before working through this self-test, we recommend you review the chapter computer labs. You should then be ready to complete the following computer objectives:
Computer Objective 1. Conduct correlation analysis. Create scatterplot between two variables; compute and interpret correlation coefficient; compute the P‑value for a two tailed hypothesis test regarding correlation.
Computer Objective 2. Conduct linear regression analysis: determine the regression equation; create a fitted plot; display the coefficient of determination; compute the P‑value for testing the significance of the regression equation; construct prediction intervals.
Computer Objective 3. Conduct the Chi-Square Hypothesis Test of Independence.
Computer Objective 4. Conduct the One Way Analysis of Variance (ANOVA) Hypothesis Test.
Instructions
Use StatCrunch and a single Word file to generate and save all of your solutions.
- Create your word processing document and call it Self‑Test6B. Save all your solutions in this file. (Be sure to use a word processing software that will allow you to later convert your document to PDF.)
- Type the main heading Self‑Test6B.
- Type the problem subheadings (Problem 1a, Problem 4b, etc.) into the file.
- As you work through the self-test computer problems, use StatCrunch to generate all computer-related solutions. Do not round off the results you get from StatCrunch.
- For each computer problem, copy and paste the output generated by StatCrunch into the Word file Self‑Test6B.
- Type your solutions to the interpretation questions into the Word file Self‑Test6B.
- Each time you make a change to a StatCrunch file or to your Word file, remember to save.
- Check your solutions. For the final solution to each problem, as well as key guided solution steps, see Self‑Test6B Solutions.
- We suggest that you print the problems and insert them in your notes. This will help you prepare for your assignments and your exams.
Self-Test 6B Problems
Note: Where relevant, do NOT round off the results you get from StatCrunch.
Once you have worked through the problems in this self-test, see Self‑Test3B Solutions to check your work.
Problem 1. Exercise 23 from Elementary Statistics, 6th edition
Exercise 23. Maximal Strength and Sprint Performance
Data is saved in the StatCrunch data file Ex9_1-23.txt available in the StatCrunch Math216 group folder. Conduct correlation analysis as specified below. Maximum Weight Strength (X) and Sprint Performance Time (Y).
Open the StatCrunch file Ex9_1-23.txt.
- Use StatCrunch to create a Scatterplot with Maximum Weight on the X axis and Time (sprint performance) on the Y axis. Copy and paste the Scatterplot to the Word file Self‑Test6B under the subheading Problem 1a.
- Based on the Scatterplot created in 1a, does the plot suggest a positive or negative correlation between Weight and Time? Type your answer in the Word file Self‑Test6B under the subheading Problem 1b.
- Use StatCrunch to compute the Correlation Coefficient, r, between Weight and Time. Copy this into the Word file Self‑Test6B under the subheading Problem 1c.
- Interpret the Correlation Coefficient number computed in 1c in the context of the two variables, Weight and Time. Type your answer in the Word file Self‑Test6B under the subheading Problem 1d.
- At a 5% level of significance use StatCrunch to conduct the t-test to see if the population correlation coefficient, ρ, between Weight and Time, is significantly different from zero. Use the four-step P‑value approach. Copy and paste the Hypothesis Test Results window to the Word file Self‑Test6B under the subheading Problem 1e under Step 2 of the test.
Problem 2. Nurses’ Salaries
The experience (in years) of fourteen registered nurses along with their annual salaries (in thousands of dollars) is in the StatCrunch data file RNurse_Salaries.txt, available in the StatCrunch Math 216 group folder.
Open the file RNurse_Salaries.txt and use StatCrunch to do the following:
- Find the equation of the linear regression line with Years of experience being the independent variable and Annual salary being the dependent variable. Copy and paste the first screen of the Simple Linear Regression Results window to the Word file Self‑Test6B under the subheading Problem 2a. Type the linear regression equation under the pasted Simple Linear Regression Results window.
- Plot the regression line along with the Scatterplot. Copy and paste the graph in the second screen of the Simple Linear Regression Results window to the Word file Self‑Test6B under the subheading Problem 2b.
- What does the slope of the regression line suggest about the relationship between the two variables? Type your answer in the Word file Self‑Test6B under the subheading Problem 2c.
- Compute the Coefficient of Determination, r-squared. Based on the Simple Linear Regression Results window pasted from 2a, type the Coefficient of Determination, r-squared, into the Word file Self‑Test6B under the subheading Problem 2d.
- Interpret the Coefficient of Determination number computed in 2d. Type your answer in the Word file Self‑Test6B under the subheading Problem 2e.
- At the 5% level of significance, test to see if the slope of the regression line significantly exceeds zero. Use the four-step P‑value approach. Based on the Simple Linear Regression Results window pasted from 2a, type the P‑value in the Word file Self‑Test6B under the subheading Problem 2f, under Step 2 of the hypothesis test.
- Construct a 95% prediction interval for the annual salary for a registered nurse with 11 years of experience. Based on the Simple Linear Regression Results window from 2a, type the prediction interval in the Word file Self‑Test6B under the subheading Problem 2g.
- Type the single prediction estimate for the annual salary for a registered nurse with 11 years of work experience in the Word file Self‑Test6B under the subheading Problem 2h.
Problem 3. Funland
Funland, an indoor amusement park located in a large mall, offers midway rides, games, fast foods, and beverages. The owners of Funland distributed the questionnaire, described below, to its regular customers. Twenty-five regular customers responded to this survey, and their responses are stored in the data file Funland, available in the StatCrunch Math 216 group folder.
Funland Questionnaire:
| Please circle the survey code or fill in the numeric amounts that apply to you below. |
Variable | Text Code |
| 1. Please indicate your marital status. | Marital | |
| ☐ single | 1 | |
| ☐ married | 2 | |
| 2. Please indicate your gender. | Gender | Code |
| ☐ female | 1 | |
| ☐ male | 2 | |
| 3. Do you frequently bring children to Funland? | Child | Code |
| ☐ yes | 1 | |
| ☐ no | 2 | |
| 4. Do you purchase a monthly pass? | Pass | Code |
| ☐ yes | 1 | |
| ☐ no | 2 | |
| Variable | Numeric Value | |
| 5. On a typical visit, please estimate the amount that you spent at Funland. |
Spend | $ _______ |
| 6. How many times per month do you typically visit Funland? | Visits | _______ |
| 7. Please indicate your monthly family income before taxes. | Income | $ _______ |
| 8. Please indicate your age. | Age | _______ |
Open the StatCrunch data file Funland and do the following.
- Use StatCrunch to create a contingency table for the survey responses in the Funland data file, with Recode(Marital) displayed as the row variable, and Recode(Pass) displayed as the column variable. Copy and paste the contingency table to the Word file Self‑Test6B under the subheading Problem 3a.
- Use the contents of the Chi-Square Test table to conduct a test of hypothesis, at a 5% level of significance, to determine whether the variables Recode(Marital) and Recode(Pass) are independent or related. Use the four-step P‑value approach. Type the Chi-Square Test Statistic and related P‑value in Step 2 of the test in the Word file Self‑Test6B under the subheading Problem 3b.
- Use the row percents displayed in the second column (Yes column) of the contingency table to describe the relationship between the variables Recode(Marital) and Recode(Pass). Type your answer in the Word file Self‑Test6B under the subheading Problem 3c.
- Comment on the expected frequency assumption underlying the Chi-square test used in independence test used in Problem 3b. Type your comments in the Word file Self‑Test6B under the subheading Problem 3d.
Problem 4. Exercise 14 from Elementary Statistics, 6th edition
Exercise 14. Housing Prices
The data file Ex10_4-14.txt, available in the StatCrunch Math216 group folder, displays the sale prices (in thousands) of a sample of one-family houses in three cities: Gainesville, Orlando, and Tampa. Open this StatCrunch data file and answer the following:
- Conduct an ANOVA test of hypothesis to see if at least one city’s mean sale price is different from the mean sales prices in the other cities surveyed, at a 10% level of significance. Use the four-step P‑value approach. Copy the ANOVA Results Table under Step 2 of the ANOVA test in the Word file Self‑Test6B under the subheading Problem 4a.
- Test the assumption of equal variances at a 5% level of significance. Use the four-step P‑value approach. Copy and paste the table displaying the Levene’s Test For Homogeneity of Variance to the Word file Self‑Test6B under the subheading Problem 4b, under Step 2 of the test.
- Use the Shapiro-Wilk Test for Normality to determine if each of the 3 samples in the data file Ex10_4-14.txt appears to come from a normal population. Assume a 5% level of significance for this test. Use the four-step P‑value approach. Copy and paste the Shapiro-Wilk goodness-of-fit results table to the Word file Self‑Test6B under the subheading Problem 4c, under Step 2 of the test.
